|
|
|
|
Example of an iterated deletion of dominated strategy equilibrium |
|
Consider the following game to better understand the concept of iterated elimination of strictly dominated strategies. |

|
|
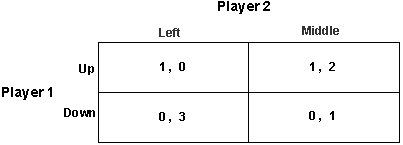
Player 1 has two strategies and player 2 has three. S1={up,down} and S2={left,middle,right}. For player 1, neither up nor down is strictly dominated. Up is better than down if 2 plays left (since 1>0), but down is better than up if 2 plays right (since 2>0). For player 2, however, right is strictly dominated by middle (since 2>1 and 1>0), so player 2 being rational will not play right. |
|
Thus if player 1 knows that player 2 is rational then player 1 can eliminate right from player 2's strategy space. So, if player 1 knows that player 2 is rational then player 1 can play the game as if it was the game depicted below. |
|
|
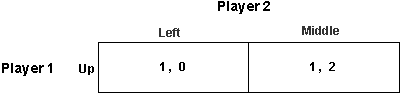
In the figure above, down is strictly dominated by up for player 1 , and so if player 1 is rational (and player 1 knows that player 2 is rational, so that the second game applies) then player 1 will not play down. Consequently, if player 2 knows that player 1 is rational, and player 2 knows that player 1 knows that player 2 is rational ( so that player 2 knows that the second game applies) then player 2 can eliminate down from player 1's strategy space, leaving the game looking like below. |
|
|
And now left is strictly dominated by middle for player 2 , leaving (up,middle) as the outcome of the game. This is process is called the iterated elimination of strictly dominated strategies. |
|
|
Page source: http://www.econport.org/econport/request?page=man_gametheory_domstrat2
|