R. Mark Issaac and James M. Walker in their classic paper "Group Size Effects in Public Goods Provision: The Voluntary Contribution Mechanism," Quarterly Journal of Economics, 53, 1988, pp.179-200, look into the relationship between variations in group size and free-riding behavior by changing the marginal return to an individual from contributions to the public good and the number of members in the group.

The Choice Environment
The Isaac and Walker experiments make use of an computerized version of the VCM. "Each individual in a group of size n faces ten "investment" periods. In each period period the experimenters endow each participant with Z_i tokens. Each token will be invested in an "individual exchange" (where it pays the individual $0.01 with certainty), or in a "group exchange""(Isaac and Walker [1988], pp. 180). The return on each token in the group exchange is equal (or directly proportional) to the sum of all individuals' contributions devided by the group size n. Each individual can decide how to divide his tokens between the two types of exchanges, but is not allowed to carry over tokens from one period to the other.

Interpreting Changes in Group Size
There are several aspects of variations in group size depending on the nature of the public good. If the public good is pure so that the rivalry in consumption is not present, increasing group size does not reduce the marginal benefit of the public good to other consumers. Impurity of the public good, meaning that it can be consumed jointly, but with crowding effect, on the other hand, causes an interaction between the number of consumers involved in the contribution process and the benefit received from its consumption.

Due to the different interpretations of group size into the laboratory experiment, the authors distinguish four relevant parameters, each being relevant for the experimental setup:
(i) marginal benefit from the individual exchange
(ii) distribution of benefits from the public goods among the consumers
(iii) the number of persons participating
(iv) the endowment of tokens to each individual

Example:
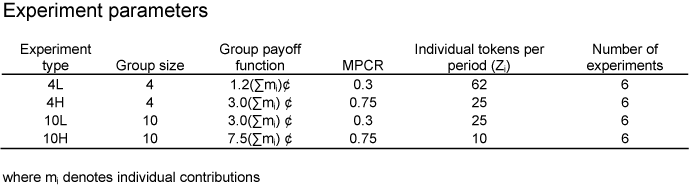
Suppose the following parametrization: n = 4, Z_i and the distribution of benefits is equal to three times the sum of all contributions (for each consumer). If the distribution of benefits is held constant, an increase in group size to ten results in decrease of marginal per capita return (MPCR) of a contribution to the public good from 0.75 to 0.3. Alternatively, the distribution of benefits could be changed as well, from 3 to 7.5, say. This approach would allow group size to increase, while holding MPCR constant at 0.75.

Based on the above characterization of the environment, Isaac and Walker identify three separate possible treatments relating the way in which a group may vary:
1. The effect of altering MPCR but holding n constant
2. The effect of altering n but adjusting the distribution of benefits so that MPCR remains constant
3. The combination effect in which altering n also alters MPCR.

Testable Predictions
The testable hypothesis is that larger groups have harder time providing the optimal level of the public good than smaller groups.

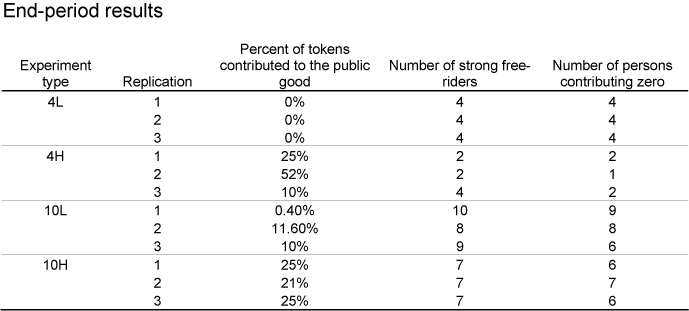
Observation 1. Lowering the MPCR from 0.75 to 0.3 significantly increases the free-riding behavior.

Observation 2. There are weak, if any, effects of changes in group size from four to ten (holding MPCR constant).

Groups with lower MPCR had more difficulty in providing Pareto efficient levels of the public good. However, when MPCR was held constant, Isaac and Walker find that changing the group size has weak and ambiguous effect, so it can be concluded that the increase in group size itself does not necessarily lead to less efficient levels of provision of the public good. However, their experimental four-treatment design allows to combine the two effects to draw one strong result: "The combined effect of the two components of group size is clearly as expected: the groups with n equal to four and with the large MPCR consistently contributed more, on average, to the public good." (Isaac and Walker [1988], pp. 193)