|
Summary. This classroom experiment involves the Stackelberg Duopoly Mini-Game (SDMG). Two players, call them Leader and Follower decide sequentially how much to produce. The Leader moves first and chooses output from two possible outputs. The Follower after observing Leader's output choice makes his output choice from a feasible set of two outputs. The total output determines the unit price and the final payoff for each player is the product of the unit price and his/her own output.
Objectives. Having students play this game first makes it easier to introduce concepts of dynamic games of perfect information and extensive form representations, and guide students' intuition towards backward induction reasoning in a natural informal way.
Requirements: Students are expected to have already been introduced to concepts of normal form game, strategy space and Nash Equilibria.
Considerations.
- The experiment can be implemented manually or computerized. The computerized version takes less time and the software organizes data instantly. To allow for learning and better understanding of playing the game students can be asked to play the game several times. Random matching is recommended at this point to keep things simpler and avoid reciprocity considerations and/or repeated game effects.
- Feasible outputs and payoffs are variable in the software, so you can choose your own figures or use the ones that appear in this document. Note that SDMG is an example of a sequential game with perfect recall, each player can move only once and there are only two feasible actions. The software for SDMG can be used for running any experiment that involves a game with two sequential moves and two possible choices for the first mover.
- After running the experiment, an informal discussion about students motivations and reasoning behind their choices can be guided towards informal introduction of backward induction reasoning.
- Elements of formal theory (such as extensive form representation of dynamic games with perfect recall (game tree, initial and terminal nodes, information sets etc.), subgames and game partition into them, backward induction as the way to analyze this game etc.) are introduced and illustrated by SDMG game.
- Finally, observed choices in the SDMG experiment are used to replicate theory.
|
|
(taken from Cox, Friedman and Sadiraj, 2006, "Revealed Altruism," Working Paper, Georgia State University)
Instructions
The Idea of the Game The game involves two players, called the Leader and the Follower, in the roles of producers of an identical good. Each decides how much to produce. The profit for each player is the number of units he decides to produce times price, net of cost. The price of the good decreases as total production increases. If you and the other player produce too much, you will drive down the price and your profits. Of course, if you don't produce much you won't have many units to sell.
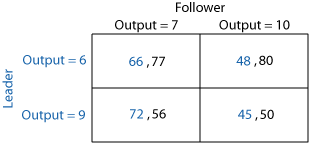
Game Details Each round the Leader chooses between two possible amounts to produce, as shown in a table with two rows. The Follower sees the choice of the Leader, and then decides among two possible amounts to produce, as shown in two columns of the same table. The table shows the profits for both players. The Leader's profit is shown in blue and it is the first entry of each box, and the Follower's profit is shown in black as the second entry. For example, in Table 1 below, if Leader chooses Output=6 and the Follower then chooses Output=7, then Leader's profit is 66 and the Follower's profit is 77.
If you are a Leader then make a choice by circling one of the rows. If you are a Follower make your choice by circling one of the cells in the row circled by the Leader.
|
|
|
Note: Payoffs in this table are derived by using the following formula. If Leader firm produces q and Follower firm produces q then the unit price is P=24- q - q, costs are set at zero, and Leader's profit is Pq whereas Follower's profit is Pq.
|
|
Strategic Form of Stackelberg Duopoly Mini-Game
|
|
|
Extensive Form of Stackelberg Duopoly Mini-Game
|
|
|
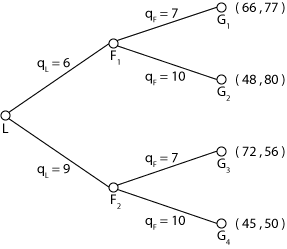
Subgame Perfect Equilibrium: {Leader chooses 9; if Leader produces 6 then Follower produces 10, if Leader produces 9 then Follower produces 7}
How would two individuals play this game if all they want is to have as much money, points as they can at the end of the game?
There can be two cases: (A) Leader chooses 6 or (B) he chooses 9.
- Leader chooses 6. Then the Follower faces the following situation. If he chooses 7 then he gets 77, if he chooses 10 then he ends up with 80. Since the Follower likes 80 more than 77 then he chooses 10 and the game ends with the Follower putting 80 in his pocket and the Leader gets 48.
- Leader chooses 9. If the Follower chooses 7 then he gets 56, if he chooses 10 then he ends up with 50. Since 56 is larger than 50 and the Follower likes the larger payoff for himself then he chooses 7 and the game ends with 56 points for the Follower and 72 points for the Leader.
Case (A) and ( B) imply that output choice of 6 units would leave the Leader with 48 points whereas a choice of 9 units would result in Leader's own payoff of 72 points. Liking 72 points more than 48 points Leader chooses to produce 9 units. This is the idea behind backward induction reasoning. You start from the end of the game (terminal nodes, G1-G4 in the tree above):
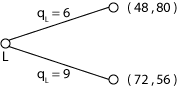
step 1: find out which terminal nodes are the preferred ones at each possible pre-nodes (F1 and F2 in the tree above);
step 2: drop branches at these nodes and write down the payoff vector that corresponds to the most preferred terminal node at that node (see the reduced form for SDMG below);
|
|
|
step 3: repeat steps 1 and 2 backwards until the initial node is reached (L in our tree).
Is this the only Nash Equilibrium in this game? No. Other Nash Equilibria are:
- {Leader chooses 9; Follower produces 7 always};
- {Leader chooses 6; Follower produces 10 always}.
Note that the Follower gets the higher payoff in the latter case, however the problem is that "Follower produces 10 always" is not a credible strategy, since were the Follower to make his output choice after observing the Leader's choice of 9 he is better off choosing 7. The problem is that {choose 10} is not a Nash equilibrium for the sub-game starting at node F2.
Other scenarios may come up following discussion after the experiment. Here are some ideas for dealing with them.
Suppose that some of the students say that their output choices were motivated by total payoffs at the terminal nodes instead of individual payoffs. What are the backward induction predictions with respect to outputs in such cases? Use the same algorithm for backward induction as just described but choose the most preferred action according to reported individual motivations. Some examples are:
- If Leader's and Follower's choices were motivated by the total payoff then {q = 6, q = 7}. Indeed, if Leader chooses 6 then the total payoffs is 143 for Follower's output choice of 7 units and 128 for Follower's output of 10 units. Liking 143 more than 128, Follower chooses to produce 7 units. Similarly, if Leader chooses to produce 9 units then the Follower chooses to produce 7 units resulting in a total payoff of 128 units. Finally, the Leader likes a total of 143 points more than a total of 128 points and therefore he chooses to produce 6 units. The Subgame Perfect Equilibrium given for individual preferences as in a) ( TODD NOTE: what is meant by "a)"? ) then is{Leader chooses to produce 6 units; Follower produces always 7 units}; in terms of outputs one has {q =6, q =7}. Similarly,
- If Follower's choice was motivated by the total payoff, Leader's choice was motivated by his own individual payoff then {q = 9, q = 7};
- If Leader's choice was motivated by the total payoff, Follower's choice was motivated by his own individual payoff then: {q = 6, q = 10};{q = 9, q = 7}.
Suggestion: Find out first what motivations were, then illustrate backward induction using objective functions following from the reported motivations.
|
| |
